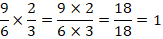Razões inversas: o que são? como determinar?

O que são razões inversas? 

Então:

Observe que o produto das alíneas c) e d) é igual a 1. Isto acontece porque as razões multiplicadas são inversas entre si: 3/4 é inversa de 4/3; 1/2 é inversa de 2/1.

Razões inversas são aquelas em que na
multiplicação entre si o resultado é sempre igual a 1. 

Quando é que duas razões são inversas entre si?

A multiplicação de uma razão pela sua inversa é sempre igual a 1.

Exemplos:

a) As razões 8/5 e 5/8 são inversas porque:

b) As razões 3/2 e 2/5 NÃO são inversas
porque:

c) As razões (9/6) “9 para 6” e “2 está para 3” (2/3) são
inversas porque:

Como determinar a inversa de uma razão?

Para determinar a inversa de uma dada razão
(a/b) basta tomar o antecedente (a) desta como consequente e o tomar o
consequente (b) como antecedente. Isto é, devemos trocar a posição
dos seus termos.

Nota: Uma razão de
antecedente zero não possui inversa.

Só é possível investir uma razão (a/b) se o antecedente for diferente de zero 0 (a≠0).

Exemplos:

a) A inversa de 6/13 é
13/6;

b) A inversa de 23/243 é 243/23;

c) A inversa de 2/7 é 7/2.

Exercícios resolvidos sobre razões inversas

 

b) 1/17

 

c) 0,5

 

d) 29%

e) (5/4) / (5/3)

e) (3/2) / (9)

PUBLICIDADE

---

Baixe também

Encontre nesta página mais Livros/ e Exames do Sistema Nacional de Ensino, e muitas outras obras importantes para o seu processo de Ensino e/ Aprendizagem

EXAMES	LIVROS	EXERCÍCIOS
BIOLOGIA	FILOSOFIA	MATEMÁTICA

Bons Estudos!