Exercício 7 de Exame de Matemática da 10ª classe 2021 (1ª Chamada)

RESOLUÇÃO DO EXERCÍCIO 7 DO EXAME DE MATEMÁTICA DA 10ª CLASSE 2021 – 1ª CHAMADA 

PUBLICIDADE

---

7. Dada a função f(x), representada no gráfico ao lado:

PUBLICIDADE

---

 

a) Quais são os zeros da função?

b) Qual é o domínio da função?

c) Qual é o contradomínio da função?

d) Qual é a ordenada na origem?

e) Qual é a variação do sinal da função?

f) Qual é a variação da função?

g) Determine a expressão analítica da função.

Resolução 

a) Quais são os zeros da função?

Indicar os zeros de uma função a partir do gráfico significa indicar os valores de x onde o gráfico (neste caso a parábola) intercepta/ corta o eixo das abcissas ou eixo dos X. 

Então temos $x_1=-3; x_2=-1$

Ou melhor os zeros desta função são $$boxed{x={-3; – 1}}$$

b) Qual é o domínio da função?

Observe que o gráfico desta função é uma parábola, e sempre que o gráfico for uma parábola voltada para cima ou para baixo, significa que se trata de uma função quadrática. 

O  domínio de uma função quadrática é sempre: $$boxed{x in R} $$. 

c) Qual é o contradomínio da função?

O contradomínio de uma função quadrática é sempre dado por:

$y in [y_V ; + infty [$ quando a parábola estiver voltada para cima 👆. 

E $y in] – infty ; y_V] $ quando a parábola estiver voltada para baixo 👇. 

Já que o gráfico dado está voltado para cima 👆e $y_V=-1$, temos que o contradomínio da função é: $$boxed{y in [-1 ; + infty [ }$$

d) Qual é a ordenada na origem?

Indicar a ordenada na origem de uma função a partir do gráfico significa indicar o valor de y onde o gráfico intercepta/ corta o eixo das ordenadas ou eixo dos Y.  

Então a ordenada na origem é $$boxed{y=3} $$

e) Qual é a variação do sinal da função?

Fazer o estudo da variação do sinal significa indicar os intervalos de X onde a função é negativa, nula ou positiva. 

Para facilitar a visibilidade usaremos a tabela. Veja a imagem👇 

PUBLICIDADE

---

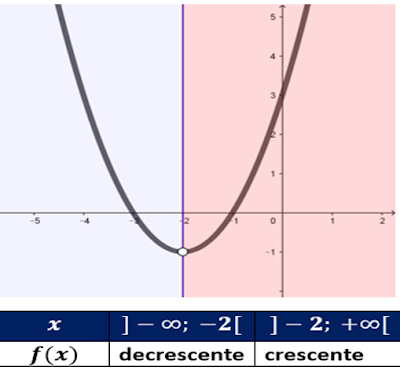
f) Qual é a variação da função?

Fazer o estudo da variação da função, ou estudo da monotonia significa indicar os intervalos de X onde a função é decrescente ou crescente. 

Para facilitar a visibilidade usaremos a tabela. Veja a imagem 👇

g) Determine a expressão analítica da função.

Usaremos os zeros da função

$x_1=-3; x_2=-1$

E o ponto $P(-2; – 1)$

Fórmula: $y=a(x-x_1)(x-x_2)$

$a=frac{y}{(x-x_1)(x-x_2)}$

Resolução 

$a=frac{-1}{(-2+3)(-2+1)}$

$a=frac{-1}{(1)(-1)}$

$a=frac{-1}{-1} a=1$

Voltando para a fórmula $y=a(x-x_1)(x-x_2)$ substituir os zeros da função e o valor do a calculado teremos:

$y=1(x+3)(x+1)$

Como o 1 é neutro na multiplicação ✖, temos. 

$y=(x+3)(x+1)$

$y=x²+1x+3x+3$

$y=x²+4x+3$

$$boxed{f(x)=x^2+4x+3}$$