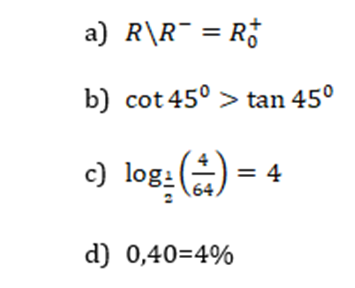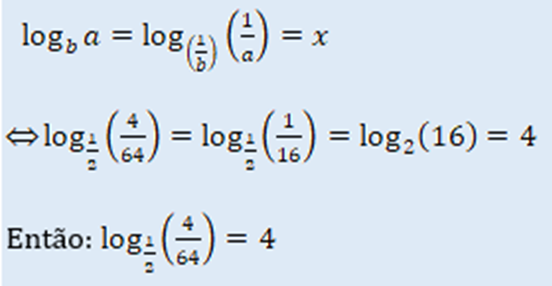RESOLUÇÃO DO EXERCÍCIO 1 DO EXAME DE MATEMÁTICA DA 10ª CLASSE 2022 – 1ª CHAMADA
1. Exercício 1: Assinale por (V) verdadeira ou por (F) falsa as seguintes afirmações que se seguem:
a) $R|R^-$
$R|R^-$ Significa $R-R^- $ (Números reais diferentes de números reais negativos)
Sabemos que conjunto R é formado por números reais negativos $(R^-)$, zero (0) e números positivos $ (R^+)$, isto é, $R= R^-U {0 } UR^{+} $ . Se tirarmos $(R^-)$ teremos como resultado o zero (0) e $(R^+)$, que formam o conjunto de números positivos incluindo o zero, chamados de números Reais Não Negativos $(R_0^+).$
Logo: a afirmação é verdadeira (V)
b) $ cot 45^0> tan 45^0$
Sabemos que $tan 45^0=cot 45^0=1$, pois este é o angulo cujo seno é igual a cosseno, e por conseguinte tangente é igual a cotangente e é sempre igual a 1.
Logo: a afirmação é Falsa (F)
c) $ log_{frac{1}{2}} (frac{4}{64})=4 $
Demostraremos a resolução de duas formas, mas antes devemos lembrar os componentes de um logaritmo.
1ª forma:
Sabemos que ao inverter a base e o logaritmando, o resultado (logaritmo) não altera:
Logo: a afirmação é verdadeira (V)
2ª forma:
Logo: a afirmação é verdadeira (V)
———————————
d) $0,40=4 %$
$0,40=40/100=40 %$ e é diferente de 4%
Logo: a afirmação é Falsa (F)